MECÂNICA GERAL
Considere a figura a seguir,
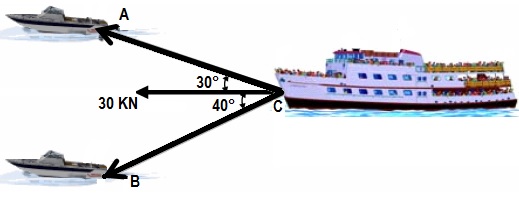
O valor aproximado dos componentes AC e BC são respectivamente
Obs.: A força de 30kN é a força resultante.
21KN e 16KN
2KN e 6KN
20KN e 26KN
29KN e 15KN
19KN e 12KN
Considere a figura abaixo. Qual a soma aproximada, dos ângulos diretores (α,β,γ,) coordenados da força resultante que atua sobre o anel?
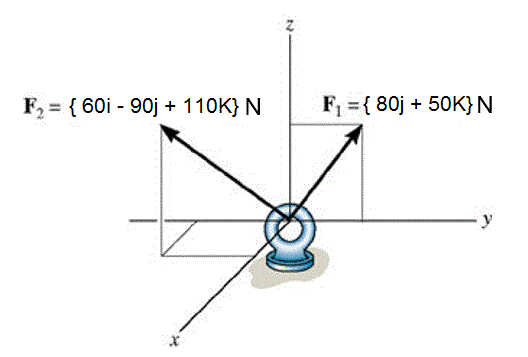
145,25°
183,76°
173,92°
231,38°
160,15°
O cabo BD exerce no poste AC uma força P dirigida ao longo de BD. Se P tem uma componente de 150N perpendicular ao poste AC, então o valor da intensidade P será aproximadamente igual a
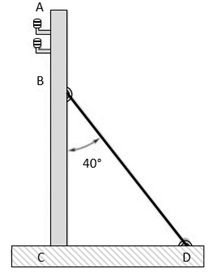
Dados: sen 40° = cos50° = 0,6428 e sen 50° = cos40° = 0,7661
233,35 N
111,12 N
213,50 N
195,82 N
215,51 N
Qual o esforço cortante e o momento em C da viga abaixo.
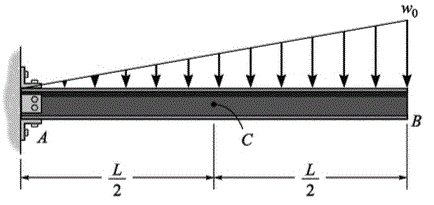
Vc = 5.wo L³/8
Mc = -9.wo L² /36
Vc = 5.wo L/8
Mc = -2.wo L² /48
Vc = 3.wo L/8
Mc = -5.wo L² /48
Vc = 4.wo L/5
Mc = -6.wo L² /36
Vc = 4.wo L²/6
Mc = -3.wo L /36
Os membros de uma treliça estão conectados à placa de ligação. Se as forças são concorrentes no ponto O, determine as intensidades de F e T para o equilíbrio. Considere o ângulo teta como sendo de 90º.
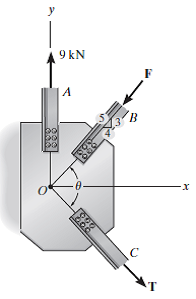
T = 6,40 kN, F = 7,50 kN
T = 7,90 kN, F = 3,40 kN
T = 6,20 kN, F = 4,40 kN
T = 7,20 kN, F = 4,70kN
T = 7,20 kN, F = 5,40 kN
A região do pé está sujeita à contração dos dois músculos plantar flexor, conforme figura abaixo,
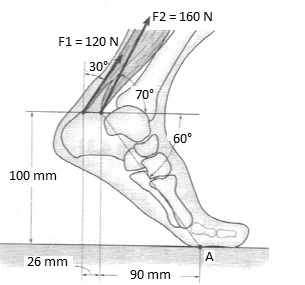
O momento de cada força em relação ao ponto de contato A no chão são respectivamente
18,80 N.m, 19,60 N.m
20 N.m, 25 N.m
18,05 N.m, 18,50 N.m
17,08 N.m, 25,4 N.m
18,05 N.m, 19 N.m
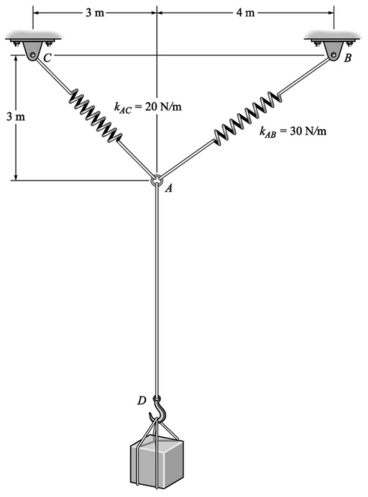
O comprimento não deformado da mola AB é 3 m. Se o bloco é mantido na posição de equílibrio mostrada, determine o peso do bloco.
83,9 N
70,7 N
80,1 N
50,6 N
60,8 N
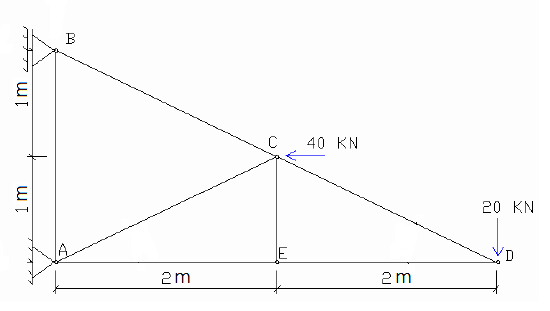
Verifique se as forças atuantes nas barras AB; AC; CD e AE; nesta sequência, se elas estão comprimindo ou tracionando a barra.
Tracionando; Comprimindo; Tracionando; Comprimindo.
Tracionando; Comprimindo; Tracionando; Tracionando.
Comprimindo; Tracionando; Tracionando; Comprimindo.
Tracionando; Comprimindo; Comprimindo; Comprimindo.
Comprimindo; Comprimindo; Tracionando; Comprimindo.
Duas forças são aplicadas a fim de remover a estaca, conforme representado na figura.
Determine o ângulo 
e o valor da força F de modo que a força resultante seja orientada verticalmente para cima no eixo y e tenha uma módulo igual a de 0,5 kN. Em seguida, marque a opção correta.
β=76,59° e F ≅ 550,45 N
β=72,89° e F ≅ 610,65 N
β=82,69° e F ≅ 570,56 N
β=70,89° e F ≅ 540,65 N
β=72,89° e F ≅ 540,65 N
Comparando a força exercida sobre a ponta do pé e calcanhar de uma mulher de 600 N nas duas situações abaixo, podemos determinar que a soma das forças normais em B nos dois casos ou seja as reações em y no ponto B nos dois casos ( By em 1 mais By em 2) é:
21KN e 16KN
2KN e 6KN
20KN e 26KN
29KN e 15KN
19KN e 12KN
Considere a figura abaixo. Qual a soma aproximada, dos ângulos diretores (α,β,γ,) coordenados da força resultante que atua sobre o anel?
145,25°
183,76°
173,92°
231,38°
160,15°
O cabo BD exerce no poste AC uma força P dirigida ao longo de BD. Se P tem uma componente de 150N perpendicular ao poste AC, então o valor da intensidade P será aproximadamente igual a
Dados: sen 40° = cos50° = 0,6428 e sen 50° = cos40° = 0,7661
233,35 N
111,12 N
213,50 N
195,82 N
215,51 N
Qual o esforço cortante e o momento em C da viga abaixo.
Vc = 5.wo L³/8
Mc = -9.wo L² /36
Vc = 5.wo L/8
Mc = -2.wo L² /48
Vc = 3.wo L/8
Mc = -5.wo L² /48
Vc = 4.wo L/5
Mc = -6.wo L² /36
Vc = 4.wo L²/6
Mc = -3.wo L /36
Os membros de uma treliça estão conectados à placa de ligação. Se as forças são concorrentes no ponto O, determine as intensidades de F e T para o equilíbrio. Considere o ângulo teta como sendo de 90º.
T = 6,40 kN, F = 7,50 kN
T = 7,90 kN, F = 3,40 kN
T = 6,20 kN, F = 4,40 kN
T = 7,20 kN, F = 4,70kN
T = 7,20 kN, F = 5,40 kN
A região do pé está sujeita à contração dos dois músculos plantar flexor, conforme figura abaixo,
O momento de cada força em relação ao ponto de contato A no chão são respectivamente
18,80 N.m, 19,60 N.m
20 N.m, 25 N.m
18,05 N.m, 18,50 N.m
17,08 N.m, 25,4 N.m
18,05 N.m, 19 N.m
O comprimento não deformado da mola AB é 3 m. Se o bloco é mantido na posição de equílibrio mostrada, determine o peso do bloco.
83,9 N
70,7 N
80,1 N
50,6 N
60,8 N
Verifique se as forças atuantes nas barras AB; AC; CD e AE; nesta sequência, se elas estão comprimindo ou tracionando a barra.
Tracionando; Comprimindo; Tracionando; Comprimindo.
Tracionando; Comprimindo; Tracionando; Tracionando.
Comprimindo; Tracionando; Tracionando; Comprimindo.
Tracionando; Comprimindo; Comprimindo; Comprimindo.
Comprimindo; Comprimindo; Tracionando; Comprimindo.
Duas forças são aplicadas a fim de remover a estaca, conforme representado na figura.
Determine o ângulo e o valor da força F de modo que a força resultante seja orientada verticalmente para cima no eixo y e tenha uma módulo igual a de 0,5 kN. Em seguida, marque a opção correta.
β=76,59° e F ≅ 550,45 N
β=72,89° e F ≅ 610,65 N
β=82,69° e F ≅ 570,56 N
β=70,89° e F ≅ 540,65 N
β=72,89° e F ≅ 540,65 N
Comparando a força exercida sobre a ponta do pé e calcanhar de uma mulher de 600 N nas duas situações abaixo, podemos determinar que a soma das forças normais em B nos dois casos ou seja as reações em y no ponto B nos dois casos ( By em 1 mais By em 2) é:
145,25°
183,76°
173,92°
231,38°
160,15°
O cabo BD exerce no poste AC uma força P dirigida ao longo de BD. Se P tem uma componente de 150N perpendicular ao poste AC, então o valor da intensidade P será aproximadamente igual a
Dados: sen 40° = cos50° = 0,6428 e sen 50° = cos40° = 0,7661
233,35 N
111,12 N
213,50 N
195,82 N
215,51 N
Qual o esforço cortante e o momento em C da viga abaixo.
Vc = 5.wo L³/8
Mc = -9.wo L² /36
Vc = 5.wo L/8
Mc = -2.wo L² /48
Vc = 3.wo L/8
Mc = -5.wo L² /48
Vc = 4.wo L/5
Mc = -6.wo L² /36
Vc = 4.wo L²/6
Mc = -3.wo L /36
Os membros de uma treliça estão conectados à placa de ligação. Se as forças são concorrentes no ponto O, determine as intensidades de F e T para o equilíbrio. Considere o ângulo teta como sendo de 90º.
T = 6,40 kN, F = 7,50 kN
T = 7,90 kN, F = 3,40 kN
T = 6,20 kN, F = 4,40 kN
T = 7,20 kN, F = 4,70kN
T = 7,20 kN, F = 5,40 kN
A região do pé está sujeita à contração dos dois músculos plantar flexor, conforme figura abaixo,
O momento de cada força em relação ao ponto de contato A no chão são respectivamente
18,80 N.m, 19,60 N.m
20 N.m, 25 N.m
18,05 N.m, 18,50 N.m
17,08 N.m, 25,4 N.m
18,05 N.m, 19 N.m
O comprimento não deformado da mola AB é 3 m. Se o bloco é mantido na posição de equílibrio mostrada, determine o peso do bloco.
83,9 N
70,7 N
80,1 N
50,6 N
60,8 N
Verifique se as forças atuantes nas barras AB; AC; CD e AE; nesta sequência, se elas estão comprimindo ou tracionando a barra.
Tracionando; Comprimindo; Tracionando; Comprimindo.
Tracionando; Comprimindo; Tracionando; Tracionando.
Comprimindo; Tracionando; Tracionando; Comprimindo.
Tracionando; Comprimindo; Comprimindo; Comprimindo.
Comprimindo; Comprimindo; Tracionando; Comprimindo.
Duas forças são aplicadas a fim de remover a estaca, conforme representado na figura.
Determine o ângulo e o valor da força F de modo que a força resultante seja orientada verticalmente para cima no eixo y e tenha uma módulo igual a de 0,5 kN. Em seguida, marque a opção correta.
β=76,59° e F ≅ 550,45 N
β=72,89° e F ≅ 610,65 N
β=82,69° e F ≅ 570,56 N
β=70,89° e F ≅ 540,65 N
β=72,89° e F ≅ 540,65 N
Comparando a força exercida sobre a ponta do pé e calcanhar de uma mulher de 600 N nas duas situações abaixo, podemos determinar que a soma das forças normais em B nos dois casos ou seja as reações em y no ponto B nos dois casos ( By em 1 mais By em 2) é:
233,35 N
111,12 N
213,50 N
195,82 N
215,51 N
Qual o esforço cortante e o momento em C da viga abaixo.
Vc = 5.wo L³/8
Mc = -9.wo L² /36
Vc = 5.wo L/8
Mc = -2.wo L² /48
Vc = 3.wo L/8
Mc = -5.wo L² /48
Vc = 4.wo L/5
Mc = -6.wo L² /36
Vc = 4.wo L²/6
Mc = -3.wo L /36
Os membros de uma treliça estão conectados à placa de ligação. Se as forças são concorrentes no ponto O, determine as intensidades de F e T para o equilíbrio. Considere o ângulo teta como sendo de 90º.
T = 6,40 kN, F = 7,50 kN
T = 7,90 kN, F = 3,40 kN
T = 6,20 kN, F = 4,40 kN
T = 7,20 kN, F = 4,70kN
T = 7,20 kN, F = 5,40 kN
A região do pé está sujeita à contração dos dois músculos plantar flexor, conforme figura abaixo,
O momento de cada força em relação ao ponto de contato A no chão são respectivamente
18,80 N.m, 19,60 N.m
20 N.m, 25 N.m
18,05 N.m, 18,50 N.m
17,08 N.m, 25,4 N.m
18,05 N.m, 19 N.m
O comprimento não deformado da mola AB é 3 m. Se o bloco é mantido na posição de equílibrio mostrada, determine o peso do bloco.
83,9 N
70,7 N
80,1 N
50,6 N
60,8 N
Verifique se as forças atuantes nas barras AB; AC; CD e AE; nesta sequência, se elas estão comprimindo ou tracionando a barra.
Tracionando; Comprimindo; Tracionando; Comprimindo.
Tracionando; Comprimindo; Tracionando; Tracionando.
Comprimindo; Tracionando; Tracionando; Comprimindo.
Tracionando; Comprimindo; Comprimindo; Comprimindo.
Comprimindo; Comprimindo; Tracionando; Comprimindo.
Duas forças são aplicadas a fim de remover a estaca, conforme representado na figura.
Determine o ângulo e o valor da força F de modo que a força resultante seja orientada verticalmente para cima no eixo y e tenha uma módulo igual a de 0,5 kN. Em seguida, marque a opção correta.
β=76,59° e F ≅ 550,45 N
β=72,89° e F ≅ 610,65 N
β=82,69° e F ≅ 570,56 N
β=70,89° e F ≅ 540,65 N
β=72,89° e F ≅ 540,65 N
Comparando a força exercida sobre a ponta do pé e calcanhar de uma mulher de 600 N nas duas situações abaixo, podemos determinar que a soma das forças normais em B nos dois casos ou seja as reações em y no ponto B nos dois casos ( By em 1 mais By em 2) é:
Vc = 5.wo L³/8 Mc = -9.wo L² /36
Vc = 5.wo L/8 Mc = -2.wo L² /48
Vc = 3.wo L/8 Mc = -5.wo L² /48
Vc = 4.wo L/5 Mc = -6.wo L² /36
Vc = 4.wo L²/6 Mc = -3.wo L /36
Os membros de uma treliça estão conectados à placa de ligação. Se as forças são concorrentes no ponto O, determine as intensidades de F e T para o equilíbrio. Considere o ângulo teta como sendo de 90º.
T = 6,40 kN, F = 7,50 kN
T = 7,90 kN, F = 3,40 kN
T = 6,20 kN, F = 4,40 kN
T = 7,20 kN, F = 4,70kN
T = 7,20 kN, F = 5,40 kN
A região do pé está sujeita à contração dos dois músculos plantar flexor, conforme figura abaixo,
O momento de cada força em relação ao ponto de contato A no chão são respectivamente
18,80 N.m, 19,60 N.m
20 N.m, 25 N.m
18,05 N.m, 18,50 N.m
17,08 N.m, 25,4 N.m
18,05 N.m, 19 N.m
O comprimento não deformado da mola AB é 3 m. Se o bloco é mantido na posição de equílibrio mostrada, determine o peso do bloco.
83,9 N
70,7 N
80,1 N
50,6 N
60,8 N
Verifique se as forças atuantes nas barras AB; AC; CD e AE; nesta sequência, se elas estão comprimindo ou tracionando a barra.
Tracionando; Comprimindo; Tracionando; Comprimindo.
Tracionando; Comprimindo; Tracionando; Tracionando.
Comprimindo; Tracionando; Tracionando; Comprimindo.
Tracionando; Comprimindo; Comprimindo; Comprimindo.
Comprimindo; Comprimindo; Tracionando; Comprimindo.
Duas forças são aplicadas a fim de remover a estaca, conforme representado na figura.
Determine o ângulo e o valor da força F de modo que a força resultante seja orientada verticalmente para cima no eixo y e tenha uma módulo igual a de 0,5 kN. Em seguida, marque a opção correta.
β=76,59° e F ≅ 550,45 N
β=72,89° e F ≅ 610,65 N
β=82,69° e F ≅ 570,56 N
β=70,89° e F ≅ 540,65 N
β=72,89° e F ≅ 540,65 N
Comparando a força exercida sobre a ponta do pé e calcanhar de uma mulher de 600 N nas duas situações abaixo, podemos determinar que a soma das forças normais em B nos dois casos ou seja as reações em y no ponto B nos dois casos ( By em 1 mais By em 2) é:
T = 6,40 kN, F = 7,50 kN
T = 7,90 kN, F = 3,40 kN
T = 6,20 kN, F = 4,40 kN
T = 7,20 kN, F = 4,70kN
T = 7,20 kN, F = 5,40 kN
A região do pé está sujeita à contração dos dois músculos plantar flexor, conforme figura abaixo,
O momento de cada força em relação ao ponto de contato A no chão são respectivamente
18,80 N.m, 19,60 N.m
20 N.m, 25 N.m
18,05 N.m, 18,50 N.m
17,08 N.m, 25,4 N.m
18,05 N.m, 19 N.m
O comprimento não deformado da mola AB é 3 m. Se o bloco é mantido na posição de equílibrio mostrada, determine o peso do bloco.
83,9 N
70,7 N
80,1 N
50,6 N
60,8 N
Verifique se as forças atuantes nas barras AB; AC; CD e AE; nesta sequência, se elas estão comprimindo ou tracionando a barra.
Tracionando; Comprimindo; Tracionando; Comprimindo.
Tracionando; Comprimindo; Tracionando; Tracionando.
Comprimindo; Tracionando; Tracionando; Comprimindo.
Tracionando; Comprimindo; Comprimindo; Comprimindo.
Comprimindo; Comprimindo; Tracionando; Comprimindo.
Duas forças são aplicadas a fim de remover a estaca, conforme representado na figura.
Determine o ângulo e o valor da força F de modo que a força resultante seja orientada verticalmente para cima no eixo y e tenha uma módulo igual a de 0,5 kN. Em seguida, marque a opção correta.
β=76,59° e F ≅ 550,45 N
β=72,89° e F ≅ 610,65 N
β=82,69° e F ≅ 570,56 N
β=70,89° e F ≅ 540,65 N
β=72,89° e F ≅ 540,65 N
Comparando a força exercida sobre a ponta do pé e calcanhar de uma mulher de 600 N nas duas situações abaixo, podemos determinar que a soma das forças normais em B nos dois casos ou seja as reações em y no ponto B nos dois casos ( By em 1 mais By em 2) é:
18,80 N.m, 19,60 N.m
20 N.m, 25 N.m
18,05 N.m, 18,50 N.m
17,08 N.m, 25,4 N.m
18,05 N.m, 19 N.m
O comprimento não deformado da mola AB é 3 m. Se o bloco é mantido na posição de equílibrio mostrada, determine o peso do bloco.
83,9 N
70,7 N
80,1 N
50,6 N
60,8 N
Verifique se as forças atuantes nas barras AB; AC; CD e AE; nesta sequência, se elas estão comprimindo ou tracionando a barra.
Tracionando; Comprimindo; Tracionando; Comprimindo.
Tracionando; Comprimindo; Tracionando; Tracionando.
Comprimindo; Tracionando; Tracionando; Comprimindo.
Tracionando; Comprimindo; Comprimindo; Comprimindo.
Comprimindo; Comprimindo; Tracionando; Comprimindo.
Duas forças são aplicadas a fim de remover a estaca, conforme representado na figura.
Determine o ângulo e o valor da força F de modo que a força resultante seja orientada verticalmente para cima no eixo y e tenha uma módulo igual a de 0,5 kN. Em seguida, marque a opção correta.
β=76,59° e F ≅ 550,45 N
β=72,89° e F ≅ 610,65 N
β=82,69° e F ≅ 570,56 N
β=70,89° e F ≅ 540,65 N
β=72,89° e F ≅ 540,65 N
Comparando a força exercida sobre a ponta do pé e calcanhar de uma mulher de 600 N nas duas situações abaixo, podemos determinar que a soma das forças normais em B nos dois casos ou seja as reações em y no ponto B nos dois casos ( By em 1 mais By em 2) é:
83,9 N
70,7 N
80,1 N
50,6 N
60,8 N
Verifique se as forças atuantes nas barras AB; AC; CD e AE; nesta sequência, se elas estão comprimindo ou tracionando a barra.
Tracionando; Comprimindo; Tracionando; Comprimindo.
Tracionando; Comprimindo; Tracionando; Tracionando.
Comprimindo; Tracionando; Tracionando; Comprimindo.
Tracionando; Comprimindo; Comprimindo; Comprimindo.
Comprimindo; Comprimindo; Tracionando; Comprimindo.
Duas forças são aplicadas a fim de remover a estaca, conforme representado na figura.
Determine o ângulo e o valor da força F de modo que a força resultante seja orientada verticalmente para cima no eixo y e tenha uma módulo igual a de 0,5 kN. Em seguida, marque a opção correta.
β=76,59° e F ≅ 550,45 N
β=72,89° e F ≅ 610,65 N
β=82,69° e F ≅ 570,56 N
β=70,89° e F ≅ 540,65 N
β=72,89° e F ≅ 540,65 N
Comparando a força exercida sobre a ponta do pé e calcanhar de uma mulher de 600 N nas duas situações abaixo, podemos determinar que a soma das forças normais em B nos dois casos ou seja as reações em y no ponto B nos dois casos ( By em 1 mais By em 2) é:
Tracionando; Comprimindo; Tracionando; Comprimindo.
Tracionando; Comprimindo; Tracionando; Tracionando.
Comprimindo; Tracionando; Tracionando; Comprimindo.
Tracionando; Comprimindo; Comprimindo; Comprimindo.
Comprimindo; Comprimindo; Tracionando; Comprimindo.
Duas forças são aplicadas a fim de remover a estaca, conforme representado na figura.
Determine o ângulo e o valor da força F de modo que a força resultante seja orientada verticalmente para cima no eixo y e tenha uma módulo igual a de 0,5 kN. Em seguida, marque a opção correta.
β=76,59° e F ≅ 550,45 N
β=72,89° e F ≅ 610,65 N
β=82,69° e F ≅ 570,56 N
β=70,89° e F ≅ 540,65 N
β=72,89° e F ≅ 540,65 N
Comparando a força exercida sobre a ponta do pé e calcanhar de uma mulher de 600 N nas duas situações abaixo, podemos determinar que a soma das forças normais em B nos dois casos ou seja as reações em y no ponto B nos dois casos ( By em 1 mais By em 2) é:
e o valor da força F de modo que a força resultante seja orientada verticalmente para cima no eixo y e tenha uma módulo igual a de 0,5 kN. Em seguida, marque a opção correta.β=76,59° e F ≅ 550,45 N
β=72,89° e F ≅ 610,65 N
β=82,69° e F ≅ 570,56 N
β=70,89° e F ≅ 540,65 N
β=72,89° e F ≅ 540,65 N